Conics in the garden

The world is made of equations if you take the time to take a closer look. My project is centered around my garden, you'll see that the math is right there in front of you if you care to take a closer look.
Ellipse
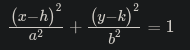
Definition: An ellipse is the set of points in a plane whose distances from two fixed points, called foci, have a constant sum.
Components: There are two axes called the major and minor axis. The major passes through the foci, center, and vertices. The minor axis runs through the center perpendicular to the major axis.
Equation: h and k represent the center (x, y) coordinates. If a > b your major axis is horizontal and if b > a the major axis is vertical. If a = b it leads to a special kind of ellipse which we will talk about later. The lengths of the major and minor axis can be found with 2 * a, and 2 * b; the larger of the two will be your major axis length. You find c by subtracting the smaller number of the denominators (c^2 = a^2 - b^2) from the other and taking the root of that number. The foci are located c units from the center along the major axis: (h +- c, k) for horizontal ellipses and (h, k +- c) for vertical.
Basil

Watering Can Base

Circle
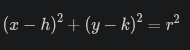
You can also use the ellipse formula because a circle is a special case of an ellipse where a = b, resulting in equal axes and a single center.
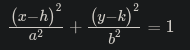
Definition: A circle is a special type of ellipse where the two focal points are the same. In the equation, this occurs when a = b.
Components: There is a center point, radius is the distance from center to the edge, and the diameter is the distance from one side to the other passing through the center.
Equation: h and k represent the center (x, y) coordinates. The radius is the r value in the equation and the diameter is 2 * r.
Peach

Pot

Table

Parabola

Definition: A parabola is the set of points in a plane that are equidistant from a fixed point called the focus and a fixed line called the directrix.
Components: The vertex is the point that is closest to the directrix and is equidistant from the focus and the directrix. The axis is perpendicular to the directrix and runs through the focus and vertex.
Equation: (x - h)^2 = 4p(y - k)” for vertical, and “(y - k)^2 = 4p(x - h) The value P cannot be 0. The vertex is at (h,k), the focus is at (h,k+p) for a vertical parabola and (h+p,k) for horizontal. Vertical directrix: y = k - p Horizontal directrix: x = h - p
Wheelbarrow

Shovel

Hyperbola
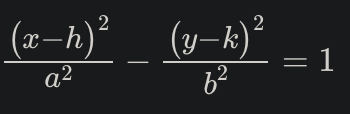
Definition: A hyperbola is the set of points in a plane whose distances from two fixed points 𝐹1 and 𝐹2 (foci) have a constant difference.
Components: The transverse axis passes through the foci and connects the center and the vertices. The conjugate axis passes through the center and is perpendicular to the major axis.
Equation: The standard form of a horizontal hyperbola is (x - h)^2/a^2 - (y - k)^2/b^2 = 1. For vertical, the y^2 term comes first. In our hyperbola equation above, it would be a horizontal hyperbola. A vertical equation would have the y squared portion first and would appear like the hose picture below. h and k still represent the center of the graph, the vertices are determined on a horizontal graph by taking the square of the denominator of the x^2 side which is "a" and adding this to h. To find the foci, use c^2 = a^2 + b^2. For a horizontal hyperbola, foci are (h +- c, k); for vertical, (h, k +- c).
Hose

Sage

Tomato

Graphs
Ellipse
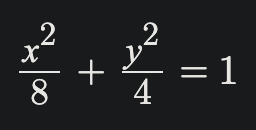

The graph is centered so (h,k) are zero. The major axis is horizontal because a > b, and the length is 2sqrt(8) units long. The minor axis is 4 units long. This makes our major vertices located at (-2sqrt(8),0) and (2sqrt(8),0) and our minor vertices at (0,-2) and (0,2). c = sqrt(a^2 - b^2), so c = sqrt(8-4) which is 2. Since this is a horizontal ellipse our foci are going to be along the x-axis, making the coordinates of our foci (-2,0) and (2,0).
Circle
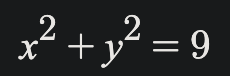
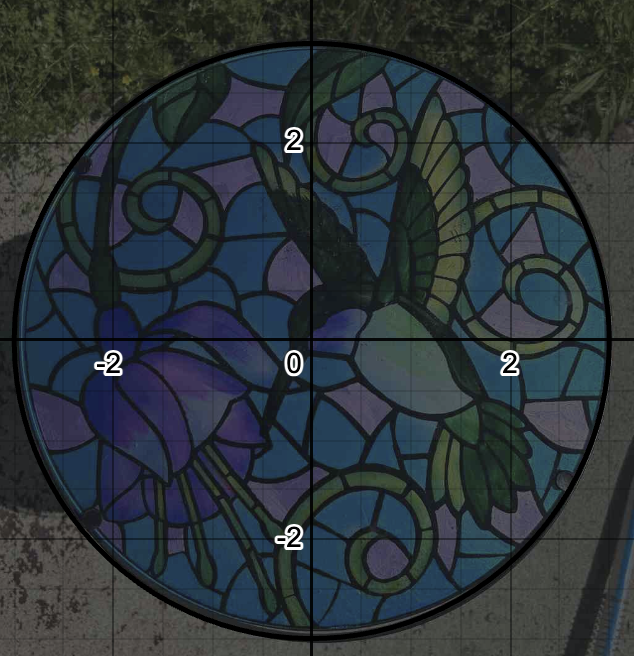
Again, our center is going to be (h,k) which is (0,0) since the image is centered. Knowing what we know about ellipses and circles, we know that the foci are going to overlap in the center making the only measurement we have left the radius which is 3. We know this because of the standard form of a circle is x^2+y^2=r^2. So the distance from the center to any given outer point of the circle is 3 units.
Conclusion
In conclusion, I never expected to find so many different examples of conics in the garden. The world around is full of mathematical equations if you look close enough. I learn through repetition and this exercise made me go through all of the equations and dive into the intricacies of each formula. There are a lot of similarities but also very subtle differences.